
2020年5月26日,港澳知名爱国企业家何鸿燊逝世,享年98岁。
提起他的名字,想必很多人都并不陌生,他大半生在澳门度过,从事博彩业近50年。博彩事业成就了何鸿燊,他也被人们称为“赌王”。
“赌王”传奇的一生不可复制,被称为赌王,也是因为他所经营的博彩事业,而非是他在赌桌上的赌技一流。
想靠赌技发家致富,那可真是件难事。是不是有很多人以为,赌博仅仅靠的是运气呢?事实上,任何一个赌徒,无论他们所谓的“运气”有多好,他都不可能靠运气赢得满桶金。因为,很难有赌徒能逃出“赌徒谬误”的魔咒。
那“赌徒谬误”是什么呢?先讲一个赌场捞金的故事。
很多人都听说过概率或统计中的蒙特·卡罗(Monte Carlo)方法,说白了就是利用大量数据在统计的基础上进行计算的方法。蒙特·卡罗不是人名,是法国边上一个袖珍小国摩纳哥的著名赌场的名字。自从蒙特·卡罗赌场于1865年开张后,摩纳哥从一个穷乡僻壤的小国,一跃成为欧洲最富有的国家之一。至今已经150年过去了,这个国家仍然以赌场和相关的旅游业为主。
当时有一个名叫约瑟夫·贾格尔(Joseph Jaggers)的英国人,是约克郡一个棉花工厂的工程师。他在摆弄加工棉花的机器之余,经常光顾蒙特·卡罗赌场,他对那种38个数字的
轮盘游戏特别感兴趣。贾格尔是位优秀的机械工程师,脑袋中的想法比一般赌徒要多一点。他想: 这个轮盘机器在理想的情况下,每个数字出现的概率都是1/38。
但是,机器怎么可能做到完美对称呢?任何缺陷都可以改变获奖号码的随机性,导致转盘停止的位置偏向某些数字,使这些数字更为频繁地出现。因此,赌徒应该可以利用这种偏向性来赚钱!于是,在1873年,贾格尔下决心要改变自己的命运。他带上所有的积蓄,前往蒙特·卡罗赌场。他雇用了6个助手,每个助手把守一个轮盘机器。
白天,赌场开放了,助手们用贾格尔供给他们的“赌币”,让轮盘不停地哗啦哗啦转!不过,他们并不在乎输赢,他们的任务是记下所把守的轮盘机停止时的每一个数字。到了晚上,赌场关门后,贾格尔便在旅馆里独自分析这些数字的规律。6天后,5个轮盘的数据没有发现有意义的偏离,但第6个轮盘为贾格尔带来了惊喜: 38个数字中有9个数出现的概率显然要比其余的频繁得多!
贾格尔兴奋不已,第7天他前往赌场,认定了那台有偏向性的轮盘机,大量投注这九个频率高的数字: 7、8、9、17、18、19、22、28和29。这种方法使贾格尔当天就赚了7万。不过,贾格尔没高兴几天,事情便引起了管理人员的注意,经理们采取了各种方法来挫败贾格尔的策略。最后贾格尔无法赚更多的钱,便离开了赌场,带着已经到手的巨款,投资房地产去了。
赌场中确有极少数人像贾格尔那样偶然幸运地赚了一笔,但更多的赌徒是十赌九输,一直到输光为止。
这其中的原因有两个: 一方面是因为所有赌场游戏的概率设计本来就是以利于赌场为准,让赌场一方赢的概率为51%或52% ,玩家赢的概率为49%或48% ,如此设计的赌场才能包赚不赔。另一方面,利用赌徒的心态也是赌博游戏设计者们的拿手好戏。赌徒谬误便是一种常见的、不符合概率规则的赌徒错误心态,经常被赌场利用。
赌徒谬误
赌徒谬误的来源是因为将前后互相独立的随机事件当成有关联而产生的。怎么样算是独立的随机事件呢?比如说,抛硬币一次,是一个随机事件;再抛一次,是另一个随机事件。两个事件独立的意思是说,第二次的结果并不依赖于第一次的结果,互相没有关联。
假设硬币是理想对称的,将出现“正”记为1,“反”记为0,那么每次结果为1和0的概率都是1/2。第二次“抛”和第一次“抛”互相独立,再多“抛”几次也一样,每次的“抛掷”事件互相独立,出现1和0的概率总是“1/2、1/2”,都和第一次一样。即使硬币不对称,比如正反面之概率可能是“2/3、1/3”,也并不会影响每次抛掷的“独立性”,每次得到正面的概率都是2/3,并不受上一次结果的影响。


道理容易懂,但有时仍会犯糊涂。
比如说,当你用“公平”硬币接连抛了5次1,到了第6次,你可能会认为这次1出现的概率更小了(<
1/2),0出现的概率更大了(>1/2)。也有人是逆向思维,认为既然5次都是1,也可能继续是1(也被称为热手谬误)。实际上这两种想法,都是掉进了“赌徒谬误”的泥坑。也就是说,将独立事件想成了互相关联事件。
事实上,一般来说,每次掷硬币的结果,并不影响下一次正反的概率。硬币没有记忆,不会因为前面5次被抛下时都是正面在上,就会加大(或减小)反面朝上的概率。也就是说,无论过去抛出的结果如何,每一次都是第一次,正反出现的概率都是1/2。
当然,认为每次抛硬币是互不关联的独立事件,也只是我们描述某些随机事件所使用的数学模型而已,物理世界中的此类事件并不一定真正独立。比如说到生男生女的问题,也许有某种与激素有关的原因使得前后两胎的性别有所关联,也不是没有这种可能性。但是,如果有关联,也要明白是如何关联的;应该使用何种模型来描述这种关联;那是另一种类型的研究课题,而赌徒谬误指的则是将基本上没有关联的随机事件认为有关联来考虑问题而产生的谬误。


赌徒有了“赌徒谬误”的心态,会输得更惨。比如说,赌场中著名的输后加倍下注系统(Martingale)便是利用赌徒谬误的例子。赌徒第一次下注1元,如输了则下注2元,再输则下注4元,如此类推,直到赢出为止,日常我们叫它直线倍投。
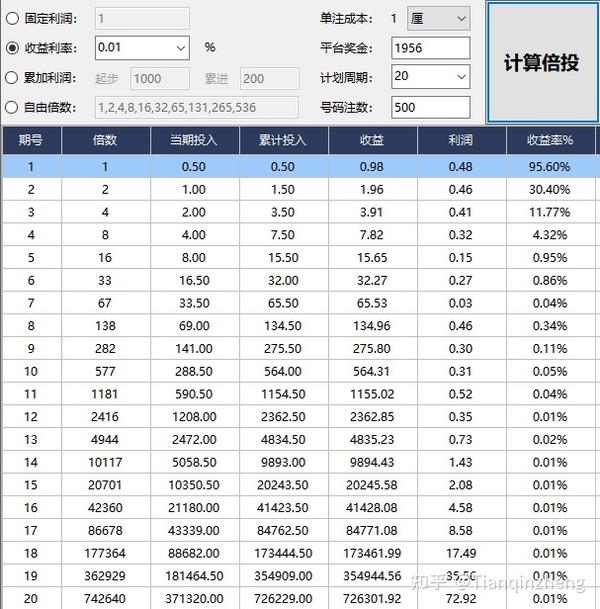

赌徒以为在连续输了多次之后,胜出的概率会非常大,所以愿意加倍又加倍地下注,殊不知其实概率是不变的,赌场的游戏机和通常抛掷的硬币一样,没有记忆,不会因为你输了就给你更多胜出的机会。赌徒或是因为不懂概率,或是因为人性的弱点,往往自觉或不自觉地陷入赌场设置的陷阱中。
赌徒谬误不仅见于赌徒,也经常反映在一般人的思维方式中。人们在预测未来时,往往倾向于把过去的历史作为判断的依据,也就是说,根据某事件曾经发生的频率来预言事件将要发生的可能性。中国人说“风水轮流转”,这句话在很多时候反映了现实,但如果将这种习惯性的思维方法随意地应用到前后互相独立的随机事件上,便成为赌徒谬误。
推荐一本书:《从掷骰子到阿尔法狗:趣谈概率》
一切都在变化,一切都难以确定,世界可以说是由变量构成,人人都有必要学点概率论,把世界看的更清晰。
书中介绍的著名趣味概率问题包括赌博点数分配问题、赌徒谬误、高尔顿钉板、几何概型悖论、酒鬼漫步、德国坦克问题、博士相亲、中国餐馆过程等。通过讨论这些简单有趣的例子,让读者了解概率统计中的重要概念,诸如随机变量、期望值、贝叶斯定理、大数定律、中心极限定理、马尔可夫过程、深度学习等等。让年轻人从游戏和趣题中学到知识,吸引他们踏进基础科学、人工智能、信息技术的大门。
回到问题本身来说,输了就是输了,老老实实打工还债吧,我相信百分之九十九点九的人,脑子加运气也是玩不过杀人不见血的大数据的,想上岸,什么是岸,岸在哪里?不赌就是岸,花点儿力气也许还有希望爬上岸。
我妈虽然是个豪爽的女汉子,但也是心思细腻的好学之人。她跟牌友们打牌从来是有输有赢,至于输赢几多,全看“火”。我爸自然是看不下去,说你们那群人打得实在太水博彩问答,我来叫你概率算牌绝学,百战百胜博彩问答,赢他们跟好玩似得,却总是被我妈不了了之。



